Suppose we need to solve the following integral...
But in this case, if we were to do that, it would actually be more work than what's necessary to
solve the integral, simply because we have this 4x term on the top.
Instead, we can rewrite this integral as...
Why? Well, 2x is the derivative of x2, and that means it will cancel that when we use a simple u-substitution. So let u = x2 + 6, and we will transform this from an integral with respect to x to an integral with respect to u.
So if we differentiate u with respect to x, we'll get du/dx = 2x. And that implies that dx = du/2x
Now, the the integral can be re-written as...
Please watch the video for the complete tutorial.


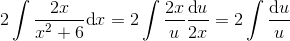
No comments:
Post a Comment